We know about factorials it is the multiplication of all integers smaller than or equal to n of a non-negative integer.

n! = (n)*(n-1)*(n-2)*.....*1

For its implementation, we just simply write a recursive function that does call back its previous integer to get multiplied and returns.

// Simple Representation in recursion
int factorial(unsigned int n)
{
    if (n == 0)
        return 1;
    return n * factorial(n - 1);
}

This above representation is known to everyone but it can only be applicable for small integers if we go to the high integers just for example of 14!, 15! or higher than this, then the above function will fail down and have a costly effect into the time and space complexity through which the error is been generated.

To overcome this for higher integers we also know about the larger factorial in GFG which is been simply multiplied according to the old school mathematics I.e we one by one multiply the number x with every digit of ans array. The digits are multiplied from the rightmost digit to the leftmost digit, as the digits are stored in reverse order.

For this the code is:

int multiplyx(int x, int ans[], int size) 
{ 
    int carry = 0;   
    for (int i=0; i<size; i++) 
    { 
        int product = ans[i] * x + carry; 
        ans[i] = product % 10;   
        carry  = product/10;     
    } 

    while (carry) 
    { 
        ans[size] = carry%10; 
        carry = carry/10; 
        size++; 
    } 
    return size; 
} 

void factorial(int n) 
{ 
    int ans[MAX]; 
    ans[0] = 1; 
    int size = 1; 
    for (int x=2; x<=n; x++) 
        size = multiplyx(x, ans, size); 
    for (int i=size-1; i>=0; i--) 
        cout << ans[i]; 
}

However, I have another process to do the similar Larger Factorials by the basic mathematics formula of Factorials approximation given by two scientists namely:

• Stirling's Approximation
• Ramanujan's Approximation

The above two approximations are very useful for a short-hand method to solve any factorial. However, these are approximation methods which is simply after 9th place of the decimal it starts fluctuating. Hopefully, we only wanted up to 3 precision(after the decimal) in the result.

1. Stirling's Approximation for Larger Factorials: is an approximation for calculating factorials. It is also useful for approximating the log of a factorial.

Formula:

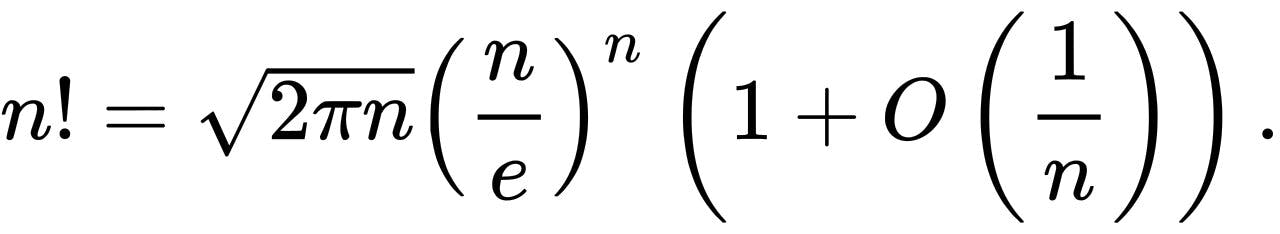
Implementation in code:

// Strling's Formula
n! =~ sqrt(2*pi*n) * pow((n/e), n)

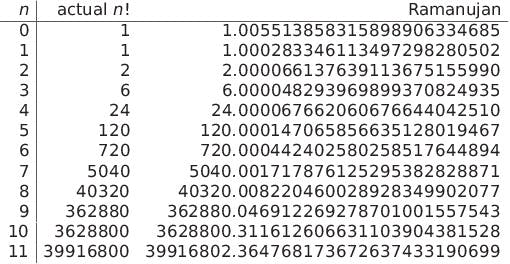
1. Ramanujan's Approximation for Larger Factorials: Ramanujan's formula is only useful for estimating what the value of n! might be for some n; and the error reduction rate appears painfully slow, slow enough to begin to accumulate error in the integer range as early as 11!; as for tweaking it, the need appears to be for an adjustment of a major sort, which perhaps I will be unable to accomplish at this time. Indeed, any adjustment that optimizes the formula over one range appears to diminish its accuracy over another, as with all asymptotic approximations of Factorial and Gamma functions in general. I'm not saying a formula for the factorial function cannot be found that is optimal for all x⩾0; I simply have neither the time nor the mathematical expertise to do it myself.

Formula:

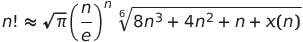
Results:

Implementation 1:

def ramanujan(x):
        fact = sqrt(pi)*(x/e)**x
        fact *= (((8*x + 4)*x + 1)*x + 1/30.)**(1./6.)
        return fact

Implementation 2:

def ramanujan2(x):
        fact = sqrt(pi)*(x/e)**x
        fact *= (((8*x + 4)*x + 1)*x + 1/30.)**(1./6.)
        if isinstance(x, int):
             fact = int(fact)
        return fact

Note: Thess formula will not give the exact value of the factorial because it is just the approximation of the factorial.